mathebellus 5
	Konstruktionen von Dreiecken und Vierecken
	Dreieckskonstruktion sws
	Dreieckskonstruktion wsw
	Bestandteile einer Konstruktion
	Konstruktionen im Maßstab
	Konstruktion von Vierecken
	Konstruktion besonderer Vierecke
	Ergänzungen

	Dreieckskonstruktion sws

Der Konstruktionstyp sws liegt vor, wenn für ein zu konstruierendes Dreieck die Längen zweier Seiten und die Größe des Winkels angegeben werden, der durch diese beiden Seiten eingeschlossen wird.

Beispielaufgabe Konstruiere ein Dreieck ABC, das folgende Maße besitzt. AB = 5,4 cm AC = 6,2 cm ∠BAC = 42° Bestimme mit Hilfe der Konstruktion die Länge der Strecke BC und die Größe des Winkels ∠CBA.	(1) Planfigur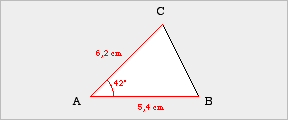
(3) Konstruktionsbeschreibung Zuerst lege ich auf einer Geraden g einen Punkt A fest. Dann markiere ich auf der gleichen Geraden g im Abstand von 5,4 cm vom Punkt A einen zweiten Punkt B. An die Halbgerade AB trage ich einen Winkel der Größe 42° an. Auf dem freien Schenkel des Winkels finde ich im Abstand von 6,4 cm vom Punkt A den Punkt C. Zuletzt zeichne ich die Strecke BC ein.	(2) Freihandskizze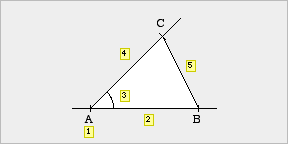
(5) Messungen BC = 4,2 cm ∠CBA = 79°	(4) Konstruktion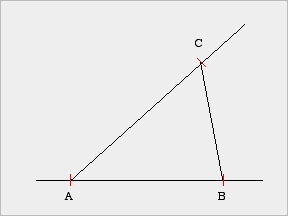

	Dreieckskonstruktion wsw

Der Konstruktionstyp wsw liegt vor, wenn für ein zu konstruierendes Dreieck die Länge einer Seite und die Größen der beiden Winkel angegeben werden, die an dieser Seite anliegen.

Beispielaufgabe Konstruiere ein Dreieck ABC, das folgende Maße besitzt. BC = 5,2 cm ∠ACB = 72° ∠CBA = 65° Bestimme mit Hilfe der Konstruktion die Länge der Strecke AB und die Größe des Winkels ∠BAC.	(1) Planfigur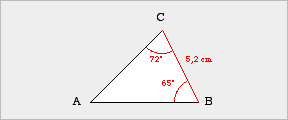
(3) Konstruktionsbeschreibung Zuerst lege ich auf einer Geraden g einen Punkt B fest. Dann markiere ich auf der gleichen Geraden g im Abstand von 5,2 cm vom Punkt B einen zweiten Punkt C. An die Halbgerade BC trage ich einen Winkel der Größe 65° an. An die Halbgerade CB trage ich einen Winkel der Größe 72° an. Als Schnittpunkt der freien Schenkel der Winkel erhalte ich den Punkt A.	(2) Freihandskizze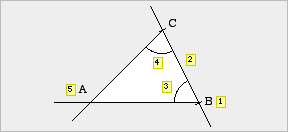
(5) Messungen AB = 7,3 cm ∠BAC = 43°	(4) Konstruktion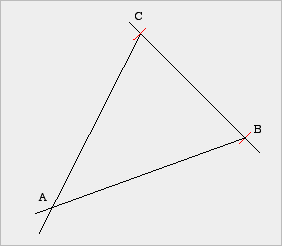

	Bestandteile der Lösung einer Konstruktionsaufgabe

(1) Planfigur

• Eine Planfigur lässt auf einen Blick erkennen, welche Stücke für eine Konstruktionsaufgabe gegeben sind; daher sind diese in der Planfigur farbig hervorgehoben und mit den gegebenen Maßen versehen.
• Auch versteckte Angaben, wie zum Beispiel rechte Winkel oder parallele Seiten, werden in der Planfigur gekennzeichnet.
  
• In der Regel sind in einer Planfigur die Eckpunkte zu bezeichnen.
• Eine Planfigur darf keine Regelmäßigkeiten aufweisen, die einen Betrachter in die Irre führen. Beispielsweise dürfen die Längen zweier Seiten oder die Größen zweier Winkel nur dann übereinstimmen, wenn diese Übereinstimmung durch die Aufgabenstellung vorgegeben ist.

(2) Freihandskizze

• Eine Freihandskizze ist eine freihändig (ohne Geo-Dreieck, ohne Lineal und ohne Zirkel) erstellte Bleistiftzeichnung, die den Ablauf der noch vorzunehmenden Konstruktion skizziert.
• In einer Freihandskizze werden die gegebenen Streckenlängen und Winkelgrößen nicht abgemessen, sondern nach Augenmaß abgeschätzt.
• Wie bei einer Konstruktion sind in einer Freihandskizze alle Konstruktionslinien hinreichend lang genug zu zeichnen. Beispielsweise muss ein freier Schenkel eines angetragenen Winkels als solcher erkennbar sein; das wäre er jedoch nicht, wenn er an einem Eckpunkt der Figur endete.
• In einer Freihandskizze werden die einzelnen Konstruktionsschritte durchnumeriert.
• Der erste Konstruktionsschritt besteht immer
• in der Festlegung einer Geraden, die die gesamte Konstruktion tragen soll, und
• in der Markierung eines Punktes auf dieser Geraden.

(3) Konstruktionsbeschreibung

• Eine Konstruktionsbeschreibung formuliert den Konstruktionsablauf in ganzen Sätzen aus, der durch die Freihandskizze festgelegt worden ist.
• Die Numerierung der Sätze entspricht der Numerierung in der Freihandskizze.
  
• Die Formulierung der Sätze erfolgt in der ersten Person („Ich-Form“) und im Präsenz.
• Da die Freihandskizze die Grundlage der Beschreibung bildet, wird in der Beschreibung kein Wort über die Handhabung der Zeichengeräte verloren. Beispielsweise sollte ein Satz wie „Ich lege den Nullpunkt des Geo-Dreiecks an den Punkt P an.“ in einer Konstruktionsbeschreibung nicht vorkommen.
  

(4) Konstruktion

• Die Konstruktion setzt den in der Freihandskizze enthaltenen Konstruktionsplan maßgenau um.
• Der erste Konstruktionsschritt besteht immer
• in der Festlegung einer Geraden, die die gesamte Konstruktion tragen soll, und
• in der Markierung eines Punktes auf dieser Geraden.
• Alle Linien werden mit Bleistift gezeichnet.
  
• Alle geraden Linien werden mit Hilfe eines Lineals oder eines Geo-Dreiecks gezeichnet.
• Alle Geraden und Halbgeraden werden so lang gezeichnet, dass sie als Geraden oder Halbgeraden auch nach Fertigstellung der Konstruktion noch deutlich erkennbar sind.
• Wird ein Punkt als Schnittpunkt zweier Linien gewonnen, so muss dieser Sachverhalt aus der Zeichnung deutlich hervorgehen.
  

	Konstruktionen im Maßstab

Der eigentliche Zweck von Konstruktionen besteht darin, wirkliche Sachverhalte zeichnerisch wiederzugeben. Da die wirklichen Längen aber häufig nicht auf einem Zeichenblatt untergebracht werden können, werden diese um einen bestimmten Faktor, dem so genannten Maßstab, verkleinert. Alle Winkelgrößen bleiben bei einer maßstäblichen Zeichnung unverändert.
Wenn aus der Zeichnung auf die Wirklichkeit zurückgeschlossen werden soll, muss der Maßstab ebenfalls berücksichtigt werden. Es ist daher zweckmäßig, eine Maßstabstabelle anzulegen, in der alle Längenentsprechungen notiert werden.

Beispiel Ein Architekt entwirft das Dach eines Einfamilienhauses; er geht von folgenden Abmessungen aus: Breite des Dachbodens: AB = 11,6 m Firsthöhe: FT = 4,6 m Position des Fußpunkts T des Firstes: AT = BT Für den Dachdecker soll er die Länge des Ortgangs AF, den Neigungswinkel des Daches  α = ∠TAF und den Firstwinkel φ = ∠BFA bestimmen.	Schaubild (Planfigur)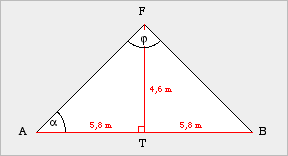
Für die zeichnerische Konstruktion legt der Architekt fest, dass ein Zentimeter in der Zeichnung einem Meter in der Wirklichkeit entsprechen soll. Dieser Maßstab wird durch die Angabe 1 cm : 1 m in der Zeichnung vermerkt. Beachte: Bei einer Maßstabsangabe wird stets zuerst die Entfernung in der Zeichnung und dann die Entfernung in der Wirklichkeit genannt.	Maßstabstabelle Zeichnung Wirklichkeit 1 cm 1 m AB 11,6 cm 11,6 m TF 4,6 cm 4,6 m AT 5,8 cm 5,8 m BT 5,8 cm 5,8 m ∠FTA 90° 90°
Konstruktionsbeschreibung Ich lege auf einer Geraden g den Punkt A fest. Im Abstand von 5,8 cm von A markiere ich auf der Geraden g den Punkt T. Wiederum im Abstand von 5,8 cm von T markiere ich auf der Geraden g den Punkt B. An die Halbgerade TA trage ich einen Winkel von 90° an. Auf dem freien Schenkel des Winkels markiere ich im Abstand von 4,6 cm von T den Punkt F. Ich zeichne die Verbindungsstrecken von T zu A und von T zu B.	Freihandskizze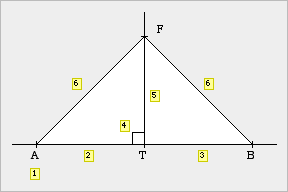
Konstruktion im Maßstab 1cm : 1m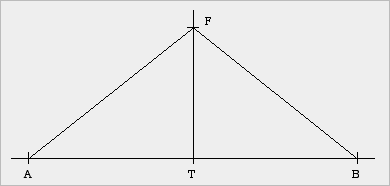	Fortsetzung der Maßstabstabelle (Angaben für den Dachdecker) Zeichnung Wirklichkeit 1 cm 1 m AF 7,4 cm 7,4 m ∠TAF 38,5° 38,5°

	Konstruktion von Vierecken

Vierecke können stets in zwei Teildreiecke zerlegt werden; daher bauen die Viereckskonstruktionen in der Regel auf den Dreieckskonstruktionen auf.

Beispielaufgabe Konstruiere ein Viereck ABCD, das folgende Maße besitzt. AB = 6,8 cm CD = 4,4 cm ∠BAC = 36° ∠CBA = 82° ∠DCA = 28° Bestimme mit Hilfe der Konstruktion die Länge der Strecke AD und die Größe des Winkels ∠BAD.	(1) Planfigur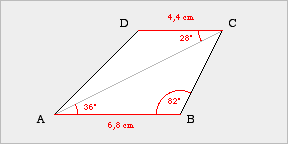
(3) Konstruktionsbeschreibung Zuerst lege ich auf einer Geraden g einen Punkt A fest. Dann markiere ich im Abstand von 6,8 cm vom Punkt A auf der Geraden g den Punkt B. An die Halbgerade AB trage ich einen Winkel der Größe 36° an. An die Halbgerade BA trage ich einen Winkel der Größe 82° an. Die beiden freien Schenkel schneiden sich im Punkt C. An die Halbgerade CA trage ich einen  Winkel der Größe 28° an. Auf dem freien Schenkel markiere ich im Abstand von 4,4 cm vom Punkt C den Punkt D. Zuletzt zeichne ich die Strecke AD.	(2) Freihandskizze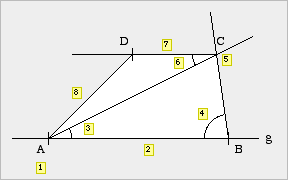
(5) Messungen AD =  4,3 cm ∠BAD = 65°	(4) Konstruktion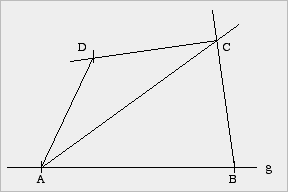

	Konstruktion besonderer Vierecke

Während für die Konstruktion eines gewöhnlichen Vierecks in der Regel fünf Stücke gegeben sein müssen, reichen für die Konstruktion gewöhnlicher Vierecke häufig deutlich weniger Angaben aus, weil zusätzlich die besonderen Eigenschaften der besonderen Vierecke bei der Konstruktion ausgenutzt werden dürfen.

Beispielaufgabe Konstruiere ein Rechteck ABCD, das folgende Maße besitzt. AC = 6,6 cm ∠CAD = 67° Bestimme mit Hilfe der Konstruktion die Seitenlängen des Rechtecks.	(1) Planfigur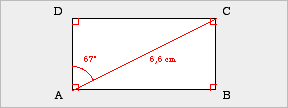
(3) Konstruktionsbeschreibung Zuerst lege ich auf einer Geraden g einen Punkt A fest. Dann markiere ich auf der Geraden g im Abstand von 6,6 cm vom Punkt A den Punkt C. An die Halbgerade AC trage ich einen  Winkel von 67° an. Vom Punkt C aus fälle ich ein Lot auf den freien Schenkel dieses Winkels. Als Lotfußpunkt erhalte ich den Punkt D. An die Halbgerade AD trage ich einen rechten Winkel an. An die Halbgerade CD trage ich einen rechten Winkel an. Der Schnittpunkt der freien Schenkel ist der Punkt B.	(2) Freihandskizze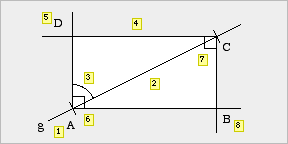
(5) Messungen AD =  2,6 cm CD =  6,1 cm	(4) Konstruktion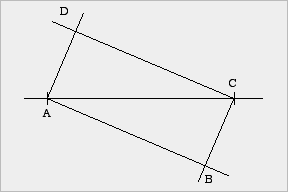

	Ergänzungen

noch nicht besetzt