mathebellus 5
	Polygone
	Definition
	Bezeichnungsweise
	Nachbarschaft
	Diagonalen, Mittellinien
	Dreiecke
	Vierecke
	Ergänzungen

	Definition

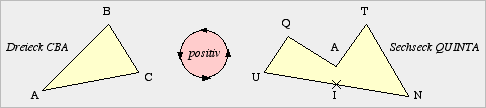
Ein Dreieck ist ein geschlossener Zug aus drei Strecken, der ein zusammenhängendes Flächenstück einschließt.
Ein Viereck ist ein geschlossener Zug aus vier Strecken, der ein zusammenhängendes Flächenstück einschließt.
Ein Fünfeck ist ein geschlossener Zug aus fünf Strecken, der ein zusammenhängendes Flächenstück einschließt.
Ist die Zahl der Strecken, die  in einem geschlossenen Zug ein zusammenhängendes Flächenstück einschließen, nicht bekannt, so spricht man von einem Polygon (Vieleck).
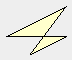
Das ist kein Polygon, weil das Flächenstück, das eingeschlossen wird, nicht zusammenhängend ist.

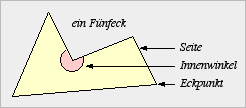
Die Endpunkte der Strecken, aus denen das Polygon gebildet wird, heißen Seiten des Polygons, ihre Endpunkte heißen Eckpunkte des Polygons.
Die Winkel an den Eckpunkten, die innerhalb des Polygons liegen, heißen Innenwinkel des Polygons.
Die Winkel an den Eckpunkten, die außerhalb des Polygons liegen, heißen nicht Außenwinkel. Der Begriff ist für andere Winkel reserviert!

	Bezeichnungsweise

Um ein Polygon zu bezeichnen, benennt man zunächst dessen Eckpunkte. Der Name des Polygons wird dann durch Hintereinanderschreiben der Namen der Eckpunkte gebildet.
Das Hintereinanderschreiben muss in der Reihenfolge eines Umlaufs geschehen, bei dem das Innere des Polygons stets links liegt.


Im gleichen Drehsinn laufen Leichtathleten um den Sportplatz; man nennt diesen Umlaufsinn „mathematisch positiv“. In diesem mathematisch positiven Sinn wird ja auch gedanklich der 1. Schenkel eines Winkels auf den 2. Schenkel gedreht.

	Nachbarschaft

Zwei Eckpunkte eines Polygons heißen benachbart, wenn sie die Endpunkte derselben Seite des Polygons sind.
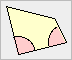
Zwei Innenwinkel eines Polygons heißen benachbart, wenn sie an benachbarten Eckpunkten des Polygons liegen.
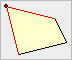
Zwei Seiten eines Polygons heißen benachbart, wenn sie einen gemeinsamen Eckpunkt haben.

	Diagonalen, Mittellinien

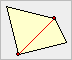
Eine Strecke, die zwei nicht benachbarte Eckpunkte verbindet, heißt Diagonale des Polygons.
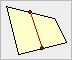
Eine Strecke, die zwei Seitenmittelpunkte verbindet, heißt Mittellinie des Polygons.

	Dreiecke

In einem Dreieck sind je zwei Eckpunkte, je zwei Innenwinkel und je zwei Seiten benachbart. Ein Dreieck besitzt keine Diagonalen. Unter den Dreiecken gibt es Sonderformen:

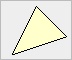
Ein Dreieck heißt spitzwinklig, wenn alle drei Innenwinkel spitze Winkel sind.
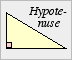
Ein Dreieck heißt rechtwinklig, wenn es einen rechten Innenwinkel besitzt. Die Seite gegenüber dem rechten Winkel heißt Hypotenuse, die anderen beiden Seiten heißen Katheten.
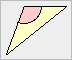
Ein Dreieck heißt stumpfwinklig, wenn es einen stumpfen Innenwinkel besitzt.
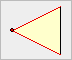
Ein Dreieck heißt gleichschenklig, wenn es zwei gleich lange Seiten besitzt. Die beiden gleich langen Seiten heißen Schenkel des Dreiecks. Die dritte Seite heißt Basis des Dreiecks. Der gemeinsame Eckpunkt der beiden Schenkel heißt Spitze des Dreiecks.
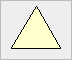
Ein Dreieck heißt gleichseitig, wenn alle drei Seiten gleich lang sind.

	Vierecke

In einem Viereck haben die nicht benachbarten Stücke einen Namen:

• Die nicht benachbarten Eckpunkte heißen gegenüberliegende Eckpunkte
• Die nicht benachbarten Innenwinkel heißen gegenüberliegende Innenwinkel.
  
• Die nicht benachbarten Seiten heißen gegenüberliegende Seiten.

Auch bei den Vierecken gibt es Sonderformen:

Ein Viereck heißt Rechteck, wenn benachbarte Seiten orthogonal zueinander sind.
Ein Viereck heißt Quadrat, wenn benachbarte Seiten orthogonal zueinander und alle Seiten gleich lang sind.
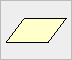
Ein Viereck heißt Parallelogramm, wenn gegenüberliegende Seiten parallel zueinander sind.
Ein Viereck heißt Raute oder Rhombus, wenn alle Seiten gleich lang sind.
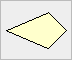
Ein Viereck heißt Drachen, wenn es aus zwei Paaren benachbarter gleich langer Seiten besitzt.
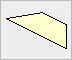
Ein Viereck heißt Trapez, wenn es ein Paar paralleler Seiten besitzt. Die parallelen Seiten heißen Grundseiten, die anderen beiden Seiten Schenkel des Trapezes.

	Ergänzungen

noch nicht besetzt