mathebellus 5
	Das Koordinatensystem
	Schatzkarten
	Definition
	Koordinaten von Punkten ablesen
	Punkte mit gegebenen Koordinaten eintragen
	Ergänzungen

	Schatzkarten

Damit der Schatz mit Hilfe der Wegbeschreibung  auf der Karte verortet werden kann, werden drei Informationen benötigt: Eine Windrose mit Himmelsrichtungen Ein Maßstab Ein Anfangspunkt Auch in der Geometrie werden diese Informationen benutzt, um die Lage von Punkten in der Ebene zu beschreiben. Der Einfachheit halber werden alle drei Elemente in einem Paar orthogonaler Geraden untergebracht. Der Schnittpunkt der beiden Geraden ist der Anfangspunkt. Die vier Halbgeraden, die durch den Schnittpunkt gebildet werden, stellen die Himmelsrichtungen dar. Der Maßstab wird durch eine Skala direkt auf den Geraden aufgebracht.

	Definition

Um die Lage eines beliebigen Punktes P in der Ebene eindeutig zu beschreiben, werden folgende Vereinbarungen getroffen:

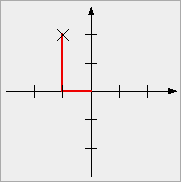
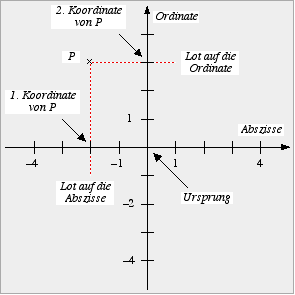
Es werden zwei Zahlengeraden festgelegt, die sich in ihren Nullpunkten orthogonal schneiden. Die beiden Zahlengeraden heißen Koordinatenachsen; ihr Schnittpunkt heißt Ursprung. Die beiden positiven Halbachsen werden mit Pfeilspitzen gekennzeichnet; sie schließen einen rechten Winkel ein. Die Achse, die den ersten Schenkel dieses Winkels bildet, heißt Abszisse, die andere Achse heißt Ordinate. Die Lage eines Punktes wird nun wie folgt bestimmt: Durch den Punkt wird eine erste Gerade gezeichnet (oder gedacht), die orthogonal zur Abzisse verläuft. Dieses Lot markiert eine Zahl auf der Abszisse. Durch den Punkt wird eine zweite Gerade gezeichnet (oder gedacht), die orthogonal zur Ordinate verläuft. Dieses Lot markiert eine Zahl auf der Ordinate. In der richtigen Reihenfolge genannt, geben die beiden Zahlen zusammen die Lage des Punktes eindeutig wieder; sie heißen Koordinaten des Punktes. Sind -2 die Abszisse  und +3 die Ordinate des Punktes P, so schreiben wir kurz P = (-2; +3) .

Dieses Verfahren zur Beschreibung der Lage der Punkte in der Ebene heißt Koordinatensystem.

	Koordinaten von Punkten ablesen

In dem nebenstehenden Schaubild ist ein geschlossener Streckenzug A-B-C-A abgebildet. Von jedem Eckpunkt aus wird je ein Lot auf die Abszisse und die Ordinate gefällt. Liegen die Koordinatenachsen auf den Linien eines Quadratgitters, so können Gitterlinien als Lote angesehen werden. Die Lote markieren Stellen auf den Achsen, die durch Zahlen dargestellt werden können. Die Lage eines jeden Punktes wird auf diese Weise durch ein Paar von Zahlen beschrieben: A = (–9; +8) B = (+3; +11) C = (–11; –3) Es wird stets die Abszisse vor der Ordinate genannt. Eselsbrücken: A kommt vor O im lateinischen Alphabet. α ist der erste, ω der letzte Buchstabe des griechischen Alphabets

	Punkte mit gegebenen Koordinaten eintragen

Beim Eintragen von Punkten ist es üblich, zuerst auf der Abszisse bis zu der Stelle zu laufen, die durch die erste Koordinate des Punktes angegeben wird. Von dort aus läuft man dann parallel zur Ordinate so weit, wie durch die zweite Koordinate vorgeschrieben wird. Das Verfahren wird mit den folgenden drei Punkten verdeutlicht: A = (–6; –11) B = (+12; –5) C = (+3; +13) D = (–10; +5)

	Ergänzungen

noch nicht besetzt