 |
mathebellus
5 |
|
| Senkrecht - Waagerecht - Orthogonal |
 |
|
| Senkrecht |
||
 |
Waagerecht |
|
 |
Orthogonal |
|
 |
Lote in der
Geometrie |
|
 |
Orthogonalität
und Parallelität |
|
 |
  |
Senkrecht |
|||
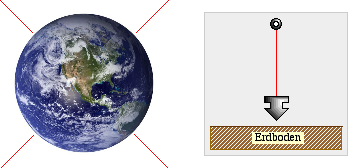 Eine Gerade verläuft senkrecht, wenn sie durch den
Mittelpunkt der Erde verläuft. Ein Stück einer solchen Geraden kann
durch ein Lot dargestellt
werden. Deswegen wird statt des Begriffes „senkrecht“ auch oft der
Begriff „lotrecht“ verwandt.
Eine Gerade verläuft senkrecht, wenn sie durch den
Mittelpunkt der Erde verläuft. Ein Stück einer solchen Geraden kann
durch ein Lot dargestellt
werden. Deswegen wird statt des Begriffes „senkrecht“ auch oft der
Begriff „lotrecht“ verwandt.Im täglichen Leben besteht ein Lot aus einer Leine, an die ein Gewicht geknüpft ist, das die Leine in Richtung des Erdmittelpunkts strafft. In der Geometrie erhält das Wort „Lot“ eine allgemeinere Bedeutung, die in einem der folgenden Abschnitte erläutert wird.
  |
Waagerecht |
|||
 Dr
Begriff waagerecht ist nicht
ganz so einfach zu erklären, wie der Begriff senkrecht. Das liegt daran, dass
eine (unendlich lange!) Gerade nicht überall, sondern nur in einem
begrenzten Abschnitt (eigentlich nur in einem Punkt) waagerecht
verlaufen kann.
Dr
Begriff waagerecht ist nicht
ganz so einfach zu erklären, wie der Begriff senkrecht. Das liegt daran, dass
eine (unendlich lange!) Gerade nicht überall, sondern nur in einem
begrenzten Abschnitt (eigentlich nur in einem Punkt) waagerecht
verlaufen kann.Eine Gerade verläuft in einem Abschnitt
AB waagerecht, wenn dieser
Abschnitt parallel zur Erdoberfläche ist.
Wenn wir daran denken, dass die Erdoberfläche gekrümmt ist, wissen wir, dass die soeben formulierte Erklärung „windig“ ist. Eigentlich müssten wir sagen:
Eine
Gerade verläuft waagerecht durch
einen Punkt P,
wenn der Punkt P von allen Geradenpunkten den kürzesten Abstand zum
Mittelpunkt der Erde hat.
Im täglichen Leben erkennen wir das Waagerechtsein einer ebenen Fläche daran, dass eine Kugel auf dem Punkt der Fläche, auf den sie gelegt wird, liegen bleibt.
Das Waagerechtsein einer Linie überprüfen wir meistens mit einer Wasserwaage. Das Röhrchen in der Libelle der Wasserwaage ist bis auf ein kleines Luftbläschen mit Flüssigkeit gefüllt. Dieses Luftbläschen wird vom Wasser in die Mitte gedrückt, wenn die Enden der Wasserwaage gleich weit vom Erdmittelpunkt entfernt sind.

  |
Orthogonal |
|||
| Wir
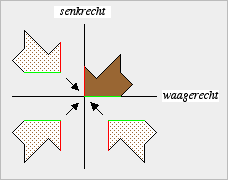
betrachten nun zwei Geraden, die sich in einem Punkt schneiden.
Verläuft eine der beiden Geraden senkrecht und die andere
Gerade waagerecht, so bilden die beiden Geraden vier gleich große Winkel. Was in der Geometrie unter einem Winkel verstanden wird, soll erst in einem der folgenden Paragraphen umfassend erklärt werden. Mit der vorangehenden Bemerkung ist hier nur Folgendes gemeint: Würden wir in einen der vier Winkel die Ecke eines Gegenstands einpassen, so würde dieser auch genau in die drei anderen Winkel passen. |
|
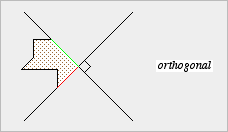
| Zwei Geraden, die vier gleich
große Winkel bilden, heißen orthogonal
(altgriechisches
Fachwort für rechtwinklig). Offenbar können Geraden auch dann orthogonal sein, wenn keine von ihnen senkrecht oder waagerecht verläuft. Nicht der Verlauf der einzelnen Geraden ist bedeutsam, sondern nur die Lage, die sie zueinander einnehmen. |
 |
Sind zwei Geraden auf ein Blatt Papier gezeichnet worden, so kann ihre auf Orthogonalität untersucht werden, indem das Papier entlang einer der beiden Geraden gefaltet wird. Die beiden Geraden sind dann orthogonal, wenn die beiden Halbgeraden, in die die andere Gerade durch die Faltgerade zerteilt wird, beim Falten exakt aufeinanderfallen.
Graphische Kennzeichnung
- Geraden, die als orthogonal angesehen werden sollen, kennzeichnen wir an ihrem Schnittpunkt durch ein kleines Quadrat.
- Sind zwei Geraden g und h orthogonal, so schreiben wir: g ⊥
h .
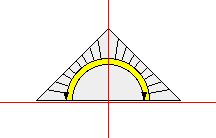
Im Geometrieunterricht verwenden wir zur Orthogonalitätsprüfung in der Regel das Geo-Dreieck. Auf dem Geo-Dreieck ist eine Linie eingedruckt, die vom Nullpunkt der Längenskala zur Spitze des Dreiecks führt. Diese Linie verläuft orthogonal zur Kante, an der die Längenskala angebracht ist.
  |
Lote in der Geometrie |
|||
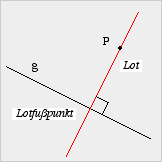 Es sei eine Gerade g und ein Punkt
P gegeben. Dann heißt diejenige Gerade, die
Es sei eine Gerade g und ein Punkt
P gegeben. Dann heißt diejenige Gerade, die- durch den Punkt P und
- orthogonal zu der Geraden g
Der Punkt, in dem das Lot die Gerade g schneidet, heißt Lotfußpunkt des Punktes P auf der Geraden g.
Es wird später gezeigt werden, dass der Lotfußpunkt derjenige Punkt der Geraden g ist, der dem Punkt P am nächsten liegt. Dewegen wird die Länge der Strecke vom Punkt zum Lotfußpunkt auch als Abstand des Punktes P von der Geraden g angesehen.
Liegt der Punkt P auf der Geraden g, so stimmt sein Lotfußpunkt mit ihm überein.
  |
Orthogonalität und
Parallelität |
|||
Die beiden Begriffe „orthogonal“ und „parallel“ hängen eng miteinander zusammen. Das wird an den beiden folgenden Theoremen („Theorem“: altgriechisches Wort für „Lehrsatz“) deutlich, die wir ohne weitere Überlegungen als richtig anerkennen wollen. Die beiden Lehrsätze sind deswegen so wichtig, weil sie uns sagen, wie wir Geraden als parallel nachweisen oder parallele Geraden zeichnen können.
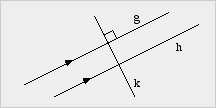 Orthogonalität
durch Parallelität
Orthogonalität
durch ParallelitätWenn eine Gerade orthogonal zu einer von zwei Parallelen ist, dann ist sie auch orthogonal zu der anderen Parallelen.
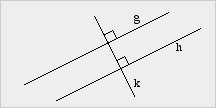 Parallelität
durch Orthogonalität
Parallelität
durch OrthogonalitätWenn zwei Geraden orthogonal zu einer dritten Geraden sind, dann sind die beiden Geraden parallel.
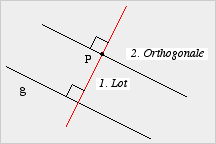 Verfahren zur Konstruktion einer
Parallelen
Verfahren zur Konstruktion einer
ParallelenSoll zu einer vorgegebenen Geraden g
eine Parallele durch einen vorgegebenen Punkt P gezeichnet werden, so
ist
- zunächst das Lot vom Punkt P auf die Gerade g zu fällen und
- dann eine Orthogonale zum Lot durch den Punkt P zu zeichnen.