mathebellus 5
	Geraden und Halbgeraden
	Geraden
	Geraden und Punkte
	Lagebeziehungen
	Halbgeraden
	Ergänzungen

	Definition des Geradenbegriffs

Eine Gerade ist eine (unendlich lange) Linie ohne Endpunkte, die folgende besondere Eigenschaft besitzt:




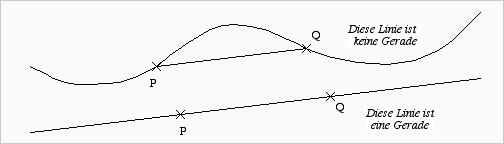
Eine Gerade kann, weil sie unendlich lang ist, ohnehin nicht vollständig gezeichnet werden; deshalb haben wir in diesem Schaubild auch darauf verzichtet, die Linie bis zum Blattrand zu zeichnen. Dass es sich um eine Gerade und nicht um eine Strecke handeln soll, erkennt man daran, dass keine Endpunkte markiert worden sind.

Bezeichnungen für Geraden:

• In der Regel kleine Druckbuchstaben verwandt: g, h, i, k, l, ...
  
  
• Reichen die Buchstaben nicht aus, können auch Indizes zu Hilfe genommen werden: g₁, g₂, g₃, ...
  
  
• Sind auf einer Geraden zwei Punkte P und Q (wie in dem Schaubild oben) festgelegt worden, so bezeichnet man die Gerade auch mit dem Symbol  PQ  (gelesen: Gerade-P-Q) oder dem Symbol QP (gelesen: Gerade-Q-P).

	Geraden und Punkte

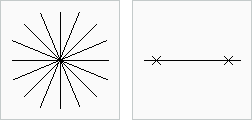Durch jeden Punkt in der Ebene verlaufen unendlich viele verschiedene Geraden. Alle Geraden, die durch einen vorgegebenen Punkt verlaufen, bilden das zu diesem Punkt gehörende Geradenbüschel.

Durch je zwei verschiedene Punkte verläuft stets nur genau eine Gerade. Auf diesen Sachverhalt haben wir bereits aufgebaut, als wir im vorangehenden Abschnitt die Bezeichnung einer Geraden mit Hilfe zweier ihrer Punkte einführten.

	Lagebeziehungen von Geraden

Für je zwei Geraden g und h trifft immer genau eine der folgenden Lagebeziehungen zu:

• g und h haben keinen gemeinsamen Punkt.
  Dann sagt man, die beiden Geraden sind parallel und schreibt kurz:  g || h .
  
  
• g und h haben genau einen gemeinsamen Punkt S.
  Dann sagt man, g und h schneiden sich im Punkt S.
  
  
• g und h haben alle Punkte gemeinsam.
  Dann sagt man, g und h sind identisch und schreibt kurz  g = h .

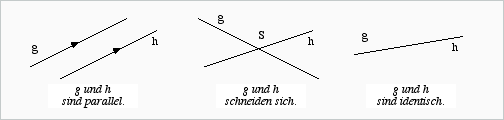
Graphische Kennzeichnung

• Zwei Geraden, die als parallel angesehen werden sollen, werden mit zwei gleich gerichteten Pfeilspitzen gekennzeichnet.
  

	Halbgeraden

Legt man auf einer Geraden einen Punkt fest, so zerteilt man damit eine Gerade in zwei Halbgeraden, die auch Strahlen genannt werden. Der zerteilende Punkt gehört zu beiden Halbgeraden; er wird Anfangspunkt der Halbgeraden genannt.


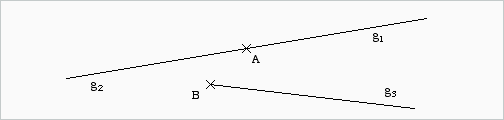
Das Schaubild zeigt insgesamt drei Halbgeraden. Zwei Halbgeraden haben denselben Anfangspunkt A. Die dritte hat einen eigenen Anfangspunkt B.

Sowohl im Punkt A als auch im Punkt B beginnen unendlich viele Halbgeraden, die hier nicht gezeichnet worden sind. Hätten wir sie alle eingezeichnet, wäre das ganze Zeichenblatt schwarz!

Unter den weiteren Halbgeraden, die im Punkt B entspringen, gibt es genau eine, die zusammen mit g₃ eine Gerade bildet. Um sie darzustellen, müsste man ein Lineal an die Gerade g₃ anlegen und dann diese Linie über den Punkt B hinaus verlängern.

Bezeichnungen für Halbgeraden:

• Es werden die gleichen kleinen Buchstaben wie für Geraden verwandt: g, h, i, k, ...
  
  
• Wie bei Geraden kommen auch oft Indizes zum Einsatz, um Halbgeraden namentlich voneinander zu unterscheiden: g₁, g₂, g₃,  ...
  
  
• Eine Halbgerade, die den Anfangspunkt R besitzt und durch den Punkt S verläuft, wird mit dem Symbol RS (gelesen: Halbgerade-R-S), nicht aber mit dem Symbol SR bezeichnet. Beispielsweise trägt in dem folgenden Schaubild die Halbgerade h den Namen BC, nicht aber den Namen CB.

	Ergänzungen

- noch unbesetzt -