mathebellus 5
	Strecken
	Linien
	Definition des Streckenbegriffs
	Länge einer Strecke
	Mittelpunkt einer Strecke
	Ergänzungen

	Linien

Wie jede andere geometrische Figur ist eine Linie eine Punktmenge. Das Besondere an einer Linie ist jedoch, dass alle ihre Punkte (wie an einer Perlenkette) lückenlos hintereinander aufgereiht sind.

Das soll die folgende Vergrößerung eines Linienstücks veranschaulichen. Diese Veranschaulichung ist aber natürlich nicht geometrisch korrekt, weil die Linienpunkte als dicke, voneinander getrennte Kleckse gezeichnet sind.

Da alle Punkte einer Linie hintereinander aufgereiht sind, muss die Breite einer Linie mit der Ausdehnung eines Punktes übereinstimmen. Nun haben wir aber verabredet, dass ein Punkt keine Ausdehnung besitzt; also hat jede Linie die Breite null. Aus diesem Grund muss man sich stets Mühe geben, alle Linien möglichst dünn zu zeichnen!

Alle Linien haben zwar dieselbe Breite, verschiedene Linien haben aber in der Regel verschiedene Längen. Falls eine Linie nicht unendlich lang ist, kann man ihre Länge messen (z.B. durch Abrollen mit einem Messrad, so wie etwa die Länge einer Straße festgestellt wird).

	Definition des Streckenbegriffs

Gegeben seien zwei Punkte A und B.
Dann ist die Strecke mit den Endpunkten A und B die kürzeste Linie, die die Punkte A und B verbindet.

Eine Strecke kann man sich stets als Faden denken, der zwischen zwei Punkten gespannt wird. Die Spannung sorgt dafür, dass der Faden möglichst kurz wird.

Strecken verkörpern das Ideal gerader Linien.

Die Strecke mit den Endpunkten A und B wird abkürzend mit dem Symbol AB (gelesen: Strecke-A-B) oder dem Symbol BA (gelesen: Strecke-B-A) bezeichnet.

	Länge einer Strecke

Eine Strecke ist eine Punktmenge. Wie jede Linie hat eine Strecke die Breite null.

Weil eine Strecke zwei Endpunkte hat, ist sie nicht unendlich lang. Also kann ihre Länge bestimmt werden. Weil eine Strecke gerade ist, kann zum Messen ihrer Länge anstelle eines Messrades die gerade Messskala auf dem Geo-Dreieck oder einem Lineal benutzt werden.

Die Länge einer Strecke AB wird wie die Strecke selber mit dem Symbol AB bezeichnet. Aus dem Zusammenhang geht stets hervor, ob die Strecke selber oder ihre Länge gemeint ist. Hat beispielsweise eine Strecke AB die Länge 4,3 cm, so schreiben wir:  AB = 4,3 cm

	Mittelpunkt einer Strecke

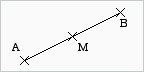Auf jeder Strecke gibt es genau einen Punkt, der die Strecke in zwei gleich lange Teilstrecken unterteilt. Dieser Punkt heißt Mittelpunkt der Strecke.

Ist beispielsweise M der Mittelpunkt der Strecke AB, so gilt:  AM = MB .

	Ergänzungen

- noch unbesetzt -