mathebellus 5
	Die Geometrische Ebene
	Begriff
	Punkte
	Bezeichnung von Punkten
	Ergänzungen

	Begriff

Die Geometrische Ebene ist eine „Idee“; sie existiert nur in unserer Vorstellung. Zur Geometrischen Ebene gibt es kein Gegenstück in der Wirklichkeit. Am ähnlichsten ist ihr noch eine spiegelglatte Wasseroberfläche.

Aber jede Wasseroberfläche auf der Erde ist durch Ufer begrenzt, während wir uns die geometrische Ebene als grenzenlos vorstellen.

Außerdem sind alle Wasseroberflächen auf der Erde gekrümmt, weil die Erde Kugelform besitzt. Das kann man gut sehen, wenn man mit einem Schiff über das Meer fährt. Die Geometrische Ebene soll aber auch keine Krümmungen aufweisen.

Wir können also nicht mit einem Beispiel aus der Wirklichkeit helfen, um die richtige Vorstellung von der geometrischen Ebene hervorzurufen. Wir können nur sagen:


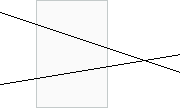Wichtig für das Weitere ist, dass wir uns ein Blatt Papier, auf dem wir geometrische Zeichnungen anfertigen, stets als Ausschnitt der geometrischen Ebene vorstellen, damit unsere Erkenntnisse nicht von der Lage und Größe unseres Zeichenblattes beeinflusst werden. Beispielsweise würden wir uns in der nebenstehenden Zeichnung von der Größe des Papiers irreführen lassen, wenn wir zu der Ansicht kämen, dass sich die beiden geraden Linien  nicht schneiden.

	Punkte

So wie sich das Bild eines Fernsehers, eines Rechnermonitors oder ein Zeitungsbild aus lauter Bildpunkten (Pixeln) zusammensetzt, so soll in unserer Vorstellung die Geometrische Ebene aus lauter Punkten bestehen.

Jede geometrische Figur besteht dann (als Teil der Ebene) wiederum aus lauter Punkten. Man spricht deshalb bei einer Figur von einer Punktmenge.

Schaut man mit einem Vergrößerungsglas auf ein Bild auf einem Rechnermonitor oder auf ein Zeitungsbild, so wird es unscharf, weil aus den winzigen Punkten kleine Quadrate oder Kreisscheiben geworden sind, deren Ausdehnung gemessen werden könnte.

Dieser Nachteil soll aber auf die geometrische Ebene nicht zutreffen. Wir verlangen von ihren Punkten, dass sie so klein sind, dass sie auch bei jeder noch so starken Vergrößerung keine Ausdehnung besitzen! Durch diese Forderung stellen wir sicher, dass eine geometrische Figur immer absolut scharf ist.

Um es noch einmal hervorzuheben: Der soeben formulierten Forderung können Punkte nur gerecht werden, wenn sie den Durchmesser 0 besitzen. Solche Punkte kann es in der Wirklichkeit nicht geben; sie sind ebenso nur eine „Idee“ wie die gesamte Geometrische Ebene.

	Bezeichnung von Punkten

Ein bestimmter Punkt der Ebene wird gekennzeichnet, indem wir zwei kurze, feine Striche zeichnen, die sich in dem zu betrachtenden Punkt schneiden. Neben das Kreuzchen schreiben wir den Namen, den wir dem markierten Punkt geben wollen.

Vereinbarung

1. Punkte werden mit großen Druckbuchstaben bezeichnet.
2. Um den Vorrat an Namen zu vergrößern, verwendet man Indizes (Plural von Index: Unterscheidungsziffer)

	Ergänzungen

- noch unbesetzt -