 |
mathebellus
5 |
|
| Multiplikation mit natürlichen Zahlen |
 |
|
| Definition |
||
 |
Begriffe |
|
 |
Das Kommutativgesetz |
|
 |
Das
Assoziativgesetz |
|
 |
Multiplikation
von natürlichen Zahlen mit negativen Zahlen |
|
 |
mathecitor
031 |
  |
Definition |
|||
Eine Zahl b wird mit einer natürlichen Zahl a multipliziert, indem sie in einer Summe a-fach aufaddiert wird:
| a • b |
= |
b + b + ...
+ b |
| a Summanden |
Beispiele
- 5 • 7 = 7 + 7 + 7 + 7 + 7 = 35
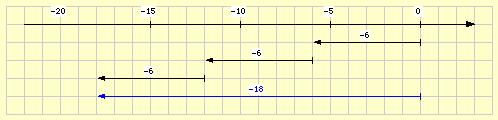
- 3 • (–6) = –6 + (–6) + (–6) = –18
Pfeildiagramm
  |
Begriffe |
|||
Das Wort „multipizieren“ ist aus der lateinischen Sprache entlehnt: „multiplicare“ bedeutet „vervielfachen“.
Die Zahlen, die an einer Multiplikation beteiligt sind, heißen „Faktoren“; das Ergebnis der Multiplikation heißt „Produkt“.
| 8 |
• |
–12 |
= |
–96 |
| Faktor |
mal |
Faktor |
gleich |
Produkt |
Das Wort „Faktor“ ist von dem lateinischen Wort „facere“ abgeleitet, welches „machen, tun“ bedeutet.
Das Wort „Produkt“ stammt von dem Wort „producere“, dem lateinischen Gegenstück zu „herstellen“, ab; „productum“ ist das „Hergestellte“.
  |
Das Kommutativgesetz (K•) |
|||
Die Reihenfolge, in der Faktoren notiert werden, beeinflusst den Wert eines Produkts nicht:
Sind a und b zwei natürliche Zahlen, so
gilt a • b = b • a .
Wir sagen: „Bei der Multiplikation natürlicher Zahlen gilt das Kommutativgesetz.“ Das Kommutativgesetz erlaubt das Vertauschen von Faktoren.
Beispiel:
a = 3 ; b = 4
| 3 • 4 = 12 |
|
4 • 3 = 12 |
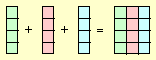 |
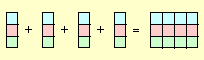 |
  |
Assoziativgesetz (A•) |
|||
Die Reihenfolge, in der Faktoren multipliziert werden, beeinflusst den Wert einer Summe nicht:
Sind a, b und c drei natürliche Zahlen,
so
gilt (a • b) • c = a • (b • c) .
Wir sagen: „Bei der Multiplikation natürlicher Zahlen gilt das Assoziativgesetz.“ Das Assoziativgesetz erlaubt das Verbinden von Faktoren zu Teilprodukten. Daher darf beim Multiplizieren die Rechenreihenfolge frei gewählt werden.
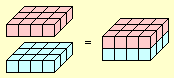
Beispiel:
a = 4 ; b = 3 ; c = 2
| (4 • 3) • 2
= 12 • 2 = 24 |
|
4 • (3 • 2)
= 4 • 6 = 24 |
 |
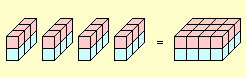 |
  |
Multiplikation von
natürlichen Zahlen mit negativen Zahlen |
|||
Wir fordern, dass das Kommutativgesetz nicht nur für die Multiplikation zweier natürlicher Zahlen (s.o.) gilt, sondern auch dann angewandt werden kann, wenn ein Faktor negativ ist.
Aus dieser Forderung können wir ableiten, was es bedeutet, eine natürliche Zahl mit einer negativen Zahl zu multiplizieren.
Beispiel:
(–7) • 9 = 9 • (–7) = –63
Auf den Fall zweier negativer Faktoren werden wir später eingehen.