mathebellus 5
Terme
Definition des Begriffs
Klammern in Termen
Klammern sparen
Termbäume
Terme mit großen Zahlen







Definition des Begriffs

Ein Term ist ein schriftlicher Ausdruck, dessen Wert berechnet werden kann.

Beispiele:
  1. (35 – 79) + a   ist ein Term.
    Vereinbaren wir, dass der Buchstabe a den Platz für die Zahl 50 hält, dann gilt:
    (35 – 79) + a = (35 – 79) + 50 = –44 + 50 = 6

  2. 68 + – ((  ist kein Term, weil
  3. |–12| – (a –b)   ist ein Term.
    Vereinbaren wir, dass a den Platz für die Zahl 144 und b den Platz für die Zahl 3 halten soll, dann gilt:
    |–12| – (a – b) = |–12| – (144 – 3) = 12 – 141 = –129

  4. #? = 45   ist kein Term, weil # und ? keine Zeichen sind, mit denen gerechnet werden kann.


Termbauregeln
  1. Folgende Elemente dürfen in einem Term auftreten:
    • Zahlen
    • Rechenzeichen
    • Klammern
    • Buchstaben, die den Platz für eine Zahl halten
    • Funktionszeichen (wie zum Beispiel Betragsstriche)
       
  2. Die Anordnung der in einem Term vorkommenden Elemente muss sinnvoll sein, wie das zweite Beispiel gezeigt hat.




Klammern in Termen

Klammern legen die Reihenfolge fest, in der die Rechenoperationen eines Terms ausgeführt werden.

Klammerregel

Rechenoperationen, die in einer Klammer stehen, sind vorrangig auszuführen.

Beispiele:
  1. 23 – (100 – 48) = 23 – 52 = –29

  2. (23 – 100) – 48 = –77 – 48 = –125

  3. 5 – (4 – (3 – 2)) = 5 – (4 – 1) = 5 – 3 = 2
Zur besseren Orientierung werden die äußeren Klammern auch eckig notiert, wenn zwei Klammerpaare ineinander geschachtelt sind:

5 – (4 – (3 – 2)) = 5 – [4 – (3 – 2)]



Klammern sparen

Die ersten beiden Beispiele (s.o.) zeigen, dass die Rechenreihenfolge eigentlich immer durch Klammersetzung geregelt werden müsste, wenn ein Term mehr als eine Verknüpfung enthält.

(1 + ((2 + 3) + 4)) + 5) + 6

Eine solche vollständige Regelung der Rechenreihenfolge durch Klammern ist jedoch nicht nur sehr umständlich; sie ist auch immer dann überflüssig, wenn das Assoziativgesetz gilt.


1. Klammerspargesetz (Assoziativgesetz)

(a + b) + c = a + (b + c) = a + b + c



Das Assoziativgesetz sagt aus, dass der Wert eines Terms nicht von der Art der Klammersetzung abhängt; also können die Klammern auch weggelassen werden:

(1 + ((2 + 3) + 4)) + 5) + 6 = 1 + 2 + 3 + 4 + 5 + 6

Die ersten beiden beiden Beispiele (s.o.) zeigen, dass das Assoziativgesetz nicht für die Subtraktion gilt.; deshalb dürfen in dem Term

(1 – ((2 – 3) – 4)) – 5) – 6

die Klammern nicht einfach weggelassen werden. Um sich auch dann das Setzen von Klammern sparen zu können, wenn das Assoziativgesetz nicht gilt, wird folgende Regel vereinbart:


2. Klammerspargesetz (Von-Links-Nach-Rechts-Regel)

Die Rechenoperationen eines Terms werden von links nach rechts ausgeführt, wenn die Rechenreihenfolge nicht durch Klammern vorgeschrieben wird.



Mit dieser Regel können auch in Subtraktionstermen all jene Klammern gespart werden, die nur die Von-Links-Nach-Rechts-Regel ausdrücken.

(1 – ((2 – 3) – 4)) – 5) – 6  = 1 – (2 – 3 – 4) – 5 – 6

Das letzte verbleibende Klammerpaar muss in diesem Beispiel stehen bleiben, weil es erzwingen soll, dass die Von-Links-Nach-Rechts-Regel durchbrochen wird.

Die Von-Links-Nach-Rechts-Regel passt zur Interpretation der Subtraktion als Additon. Wird die Subtraktion als Addition interpretiert, erhält man dasselbe Ergebnis wie bei einer Rechnung „von links nach rechts“.

Beispiel:

23 – 100 – 48 = –77 – 48 = –125    („Von links nach rechts”)

23 – 100 – 48 = 23 + (–100) + (–48) = [23 + (–100)] + (–48) = –77 + (–48) = –125
23 – 100 – 48 = 23 + (–100) + (–48) = 23 + [(–100) + (–48)] = 23 + (–148) = –125


Im Zusammenhang mit den Punktrechenarten wird spätere eine weitere Klammersparregel eingeführt und erläutert werden; diese wird hier nur der Vollständigkeit halber erwähnt.


3. Klammerspargesetz („Punktrechnung vor Strichrechnung“)

Treten in einem Term Punkt- und Strichrechnungen auf, sind die Punktrechnungen vorrangig auszuführen, wenn nicht Klammern eine andere Reihenfolge vorschreiben.





Termbäume

Mit Hilfe von Termbäumen kann der rechnerische Aufbau eines Terms grafisch veranschaulicht werden:




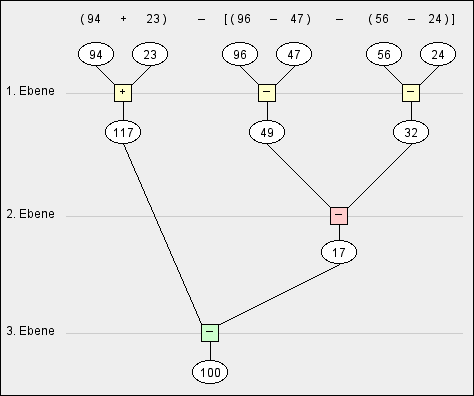
Erläuterung:

Die Berechnung ohne einen Baum erfolgt auf gleiche Weise:

(94 + 23) – [(96 – 47) – (56 – 24)]
= 117 – [49 – 32]
= 117 – 17
= 100

Bei der Berechnung eines Terms ist ein Missbrauch des Gleichheitszeichens zu vermeiden; die folgende Rechnung enthält vier ungültige Gleichheitszeichen!

(94 + 23) – [(96 – 47) – (56 – 24)]
= 96 – 47 = 49 = 56 – 24 = 32 = 49 – 32 = 17
= 117 – 17
= 100




Terme mit großen Zahlen

Terme mit großen Zahlen werden grundsätzlich auf gleiche Weise fortlaufend berechnet, wie es in dem vorangehenden Abschnitt gezeigt wurde. Die erforderlichen Nebenrechnungen werden deutlich sichtbar ausgelagert:

   –3465 – [–1298 + (– 3461 + 9658)] = –3465 – [–1298 + 6197] = –3465 – 4899 = –8364




Wichtige Hinweise: