 |
mathebellus
5 |
|
| Schriftliche Rechnung mit Beträgen (natürlichen Zahlen) |
 |
|
| Schriftliche Addition |
||
 |
Schriftliche Addition in anderen Stellenwertsystemen | |
 |
Schriftliche Subtraktion |
|
 |
Schriftliche
Subtraktion in anderen Stellenwertsystemen |
|
 |
  |
Schriftliche Addition | |||
Das Schriftliche Addieren beruht auf dem Gedanken des stellenweisen Addierens :
- Zerlege die Summanden gedanklich in Anzahlen von Stellenwerten
- Spalte von den Summanden die Anzahlen des ersten Stellenwerts
(Einer) ab und addiere sie
- Nimm einen Übertrag auf den nächsten Stellenwert (Zehner) vor, wenn die Summe der Anzahlen 10 überschreitet
- Spalte von den Summanden die Anzahlen des nächsten Stellenwerts ab, addiere sie und den Übertrag.
- Nimm erneut einen Übertrag auf den nächsten Stellenwert vor, wenn die Summe der Anzahlen 10 überschreitet
- Wiederhole die Schritte 4. und 5., bis die Summanden vollständig
addiert sind.
62783
+ 54869
(E: Einer; Z: Zehner; H: Hunderter; T: Tausender; ZT: Zehntausender; HT: Hunderttausender)
= 62780
+ 3E
+ 54860 + 9E
= 62780 + 54860 +(3E + 9E) [K+, A+]
= 62780 + 54860 + 12E
= 62780 + 54860 + 1Z + 2E
= 62700 + 8Z + 54800 + 6Z + 1Z + 2E
= 62700 + 54800 +(8Z + 6Z + 1Z) + 2E [K+, A+]
= 62700 + 54800 + 15Z + 2E
= 62700 + 54800 + 1H + 5Z + 2E
= 62000 + 7H + 54000 + 8H + 1H + 5Z + 2E
= 62000 + 54000 + (7H + 8H +1H) + 5Z + 2E [K+, A+]
= 62000 + 54000 + 16H + 5Z + 2E
= 62000 + 54000 + 1T + 6H + 5Z + 2E
= 60000 + 2T + 50000 + 4T + 1T + 6H + 5Z + 2E
= 60000 + 50000 + (2T + 4T +1T) + 6H + 5Z + 2E [K+, A+]
= 62000 + 54000 + 7T + 6H + 5Z + 2E
= 6ZT + 5ZT + 7T + 6H + 5Z + 2E
= 11ZT +7T + 6H + 5Z + 2E
= 1HT + 1ZT + 7T + 6H + 5Z + 2E
= 117652
= 62780 + 54860 +(3E + 9E) [K+, A+]
= 62780 + 54860 + 12E
= 62780 + 54860 + 1Z + 2E
= 62700 + 8Z + 54800 + 6Z + 1Z + 2E
= 62700 + 54800 +(8Z + 6Z + 1Z) + 2E [K+, A+]
= 62700 + 54800 + 15Z + 2E
= 62700 + 54800 + 1H + 5Z + 2E
= 62000 + 7H + 54000 + 8H + 1H + 5Z + 2E
= 62000 + 54000 + (7H + 8H +1H) + 5Z + 2E [K+, A+]
= 62000 + 54000 + 16H + 5Z + 2E
= 62000 + 54000 + 1T + 6H + 5Z + 2E
= 60000 + 2T + 50000 + 4T + 1T + 6H + 5Z + 2E
= 60000 + 50000 + (2T + 4T +1T) + 6H + 5Z + 2E [K+, A+]
= 62000 + 54000 + 7T + 6H + 5Z + 2E
= 6ZT + 5ZT + 7T + 6H + 5Z + 2E
= 11ZT +7T + 6H + 5Z + 2E
= 1HT + 1ZT + 7T + 6H + 5Z + 2E
= 117652
(E: Einer; Z: Zehner; H: Hunderter; T: Tausender; ZT: Zehntausender; HT: Hunderttausender)
Der Vorgang wird übersichtlicher, wenn er in einer Stellentabelle dargestellt wird:
| HT |
ZT |
T |
H |
Z |
E |
|
| 1. Summand |
6 |
2 |
7 |
8 |
3 |
|
| 2. Summand |
5 |
4 |
8 |
6 |
9 |
|
| Übertrag |
1 |
1 |
1 |
1 |
||
| Summe |
1 |
1 |
7 |
6 |
5 |
2 |
Werden die Tabellenstriche, die Zeilen- und Spaltenüberschriften weggelassen, entspricht die Darstellung in der Stellentabelle der üblichen schriftlichen Addition:
| 6 |
2 |
7 |
8 |
3 |
|
| 5 |
4 |
8 |
6 |
9 |
|
| 1 |
1 |
1 |
1 |
||
| 1 |
1 |
7 |
6 |
5 |
2 |
  |
Schriftliche Addition in anderen Stellenwertsystemen | |||
Das Verfahren der schriftlichen Addition kann ohne Einschränkungen auf andere Stellenwertsystem übertragen werden. Es ist erst dann gedanklich erfasst, wenn es auch in anderen Stellenwertsystemen angewandt werden kann.
Hier zunächst ein „pentonisches“ Beispiel:
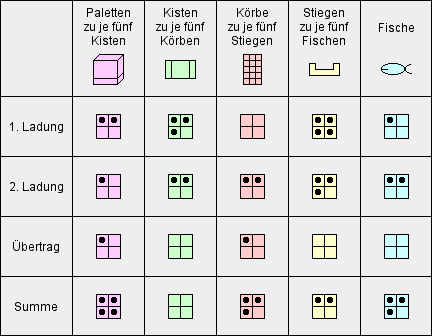
Erläuterung:
- Es werden die Ladungen zweier Fischereiboote addiert.
- Zunächst die unverpackten Fische: Weil es davon zusammen nur drei gibt, bleiben sie auch in der Summe unverpackt. Für eine Stiege wären fünf Fische erforderlich gewesen.
- Insgesamt gibt es sieben Stiegen; davon müssen fünf Stiegen in einen Korb gepackt werden, zwei bleiben übrig.
- Zusammen mit dem soeben gebildeten Korb gibt es insgesamt drei Körbe. Diese bleiben wie sie sind, denn für eine Kiste wären fünf Körbe erforderlich.
- Insgesamt gibt es fünf Kisten; mit ihnen kann genau eine Palette beladen werden. Keine Kiste bleibt übrig.
- Zusammen mit der soeben gebildeten Palette, liegen insgesamt vier
Paletten vor.
| 2 |
3 |
0 |
4 |
1 |
|
| + |
1 |
2 |
2 |
3 |
2 |
| 1 |
1 |
||||
| 4 |
0 |
3 |
2 |
3 |
Die Darstellung der Zahlen mit Hilfe von Punktbildern ist auch bei der Addition in anderen Stellenwertsystemen hilfreich. Hier ein Beispiel im 16er-System:
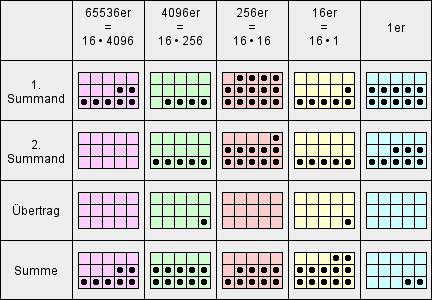
Erläuterung:
- Es liegen achtzehn Einer vor. Sechzehn Einer ergeben einen 16er.
Es bleiben zwei Einer übrig.
- Zusammen mit dem soeben gebildeten 16er gibt es zwölf 16er. Diese
bleiben wie sie sind. Zum Bilden eines 256ers müssten sechzehn 16er
vorliegen.
- Insgesamt gibt es fünfundzwanzig 256er; sechzehn 256er ergeben
einen 4096er. Es bleiben neun 256er übrig.
- Zusammen mit dem soeben gebildeten 4096er liegen zehn 4096er vor. Diese bleiben wie sie sind.
- Insgesamt gibt es sieben 65536er auch diese bleiben, wie sie sind.
Das ist die zugehörige Addition im 16er-System:
| 7 |
4 |
E |
6 |
A |
|
| + |
5 |
B |
5 |
8 |
|
| 1 |
1 |
||||
| 7 |
A |
9 |
C |
2 |
  |
Schriftliche Subtraktion | |||
Der Abschnitt ist noch nicht besetzt.
  |
Schriftliche Subtraktion in anderen Stellenwertsystemen | |||
Der Abschnitt ist noch nicht besetzt.