 |
mathebellus
5 |
|
| Addition ganzer Zahlen |
 |
|
| Darstellung der Addition mit Hilfe von
Pfeildiagrammen |
||
 |
Formale Definition | |
 |
Kommutativgesetz |
|
 |
Assoziativgesetz |
|
 |
mathecitor 021 |
  |
Darstellung der Addition mit Hilfe von Pfeildiagrammen | |||
Das Addieren ganzer Zahlen soll möglichst genauso funktionieren wie das Addieren natürlicher Zahlen.
Die Addition natürlicher Zahlen wird durch das Aneinanderhängen von Pfeilen beschrieben. Diese Beschreibung ist auch gültig für die Addition von Gegenzahlen natürlicher Zahlen, mit der die Subtraktion natürlicher Zahlen ersetzt worden ist.
Legen wir fest, dass das Addieren zweier ganzer Zahlen immer durch das Aneinanderhängen von Pfeilen beschrieben werden soll, so gründen wir die Addition auf ein einheitliches Prinzip.
Im Folgenden wird dieses Prinzip für die verschiedenen Fälle an Beispielen vorgestellt.
Fall I
Beide Summanden sind positiv.
(+7) + (+5) = (+12)
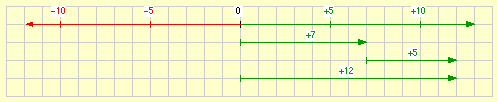
Das ist der klassische Fall der Addition zweier natürlicher Zahlen.
Kurzschreibweise: 7 + 5 = 12
Fall IIa
Der 1. Summand ist positiv, der 2.
Summand ist negativ; der Betrag des 1. Summanden ist größer.
(+11) + (–6) = (+5)
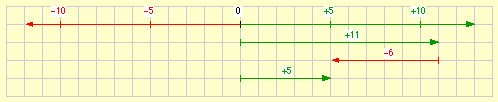
Das ist der klassische Fall der Subtraktion zweier natürlicher Zahlen mit positiver Differenz.
Kurzschreibweise: 11 – 6 = 5
Wir notieren zwar eine Subtraktion, denken uns diese jedoch als Addition einer negativen Zahl!
(+11) + (–6) = (+5)

Das ist der klassische Fall der Subtraktion zweier natürlicher Zahlen mit positiver Differenz.
Kurzschreibweise: 11 – 6 = 5
Wir notieren zwar eine Subtraktion, denken uns diese jedoch als Addition einer negativen Zahl!
Fall IIb
Der 1. Summand ist positiv, der 2.
Summand ist negativ; der Betrag des 2. Summanden ist größer.
(+9) + (–15) = (–6)

Das ist der Fall der Subtraktion zweier natürlicher Zahlen mit negativer Differenz, der die Einführung der negativen Zahlen hervorgerufen hat.
Kurzschreibweise: 9 – 15 = –6
(+9) + (–15) = (–6)

Das ist der Fall der Subtraktion zweier natürlicher Zahlen mit negativer Differenz, der die Einführung der negativen Zahlen hervorgerufen hat.
Kurzschreibweise: 9 – 15 = –6
Fall IIIa
Der 1. Summand ist negativ, der 2.
Summand ist positiv; der Betrag des 1. Summanden ist größer.
(–10) + (+7) = (–3)
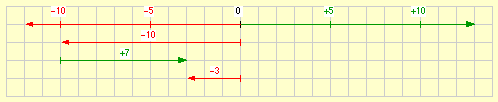
Das ist der erste neue Fall; zu einer negativen Zahl wird eine positive addiert.
Kurzschreibweise: –10 + 7 = –3
(–10) + (+7) = (–3)

Das ist der erste neue Fall; zu einer negativen Zahl wird eine positive addiert.
Kurzschreibweise: –10 + 7 = –3
Fall IIIb
Der 1. Summand ist negativ, der 2.
Summand ist positiv; der Betrag des 2. Summanden ist größer.
(–8) + (+17) = (+9)
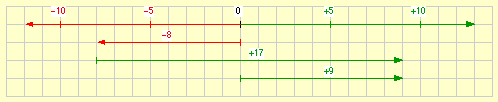
Dieser Fall unterscheidet sich von dem vorangehenden nur durch das positive Ergebnis.
Kurzschreibweise: –8 + 17 = 9
(–8) + (+17) = (+9)

Dieser Fall unterscheidet sich von dem vorangehenden nur durch das positive Ergebnis.
Kurzschreibweise: –8 + 17 = 9
Fall IV
Beide Summanden sind negativ.
(–4) + (–7) = (–11)
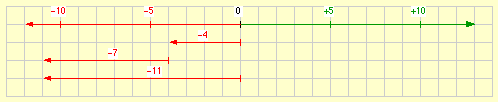
Das ist der andere neue Fall; zwei negative Zahlen werden addiert.
Kurzschreibweise: –4 – 7 = –11
(–4) + (–7) = (–11)

Das ist der andere neue Fall; zwei negative Zahlen werden addiert.
Kurzschreibweise: –4 – 7 = –11
  |
Formale Definition | |||
In jedem der sechs vorangehend beschriebenen Fälle ist (im Kopf) eine Rechnung mit den Beträgen der Summanden vorzunehmen, um die Addition der ganzen Zahlen auszuführen.
| Addition
ganzer Zahlen |
Rechnung mit
Beträgen |
| (+7) + (+5) = (+12) | 7 + 5 = 12 |
| (+11) + (–6) = (+5) | 11 – 6 = 5 |
| (+9) + (–15) = (–6) | 15 – 9 = 6 |
| (–10) + (+7) = (–3) | 10 – 7 = 3 |
| (–8) + (+17) = (+9) | 17 – 8 = 9 |
| (–4) + (–7) = (–11) | 4 + 7 = 11 |
Aus dieser Zusammenstellung ergeben sich folgende Regeln für das Addieren ganzer Zahlen:
- Haben die beiden Summanden gleiche Vorzeichen, werden ihre
Beträge addiert.
Das gemeinsame Vorzeichen der Summanden ist auch das Vorzeichen der Summe.
- Haben die beiden Summanden verschiedene Vorzeichen, werden ihre
Beträge voneinander subtrahiert.
Das Vorzeichen des Summanden mit dem größeren Betrag ist auch das Vorzeichen der Summe.
  |
Kommutativgesetz | |||
Die soeben formulierten Additionsregeln nehmen keinen Bezug auf die Reihenfolge, in der die Summanden notiert sind; nur Vorzeichen und Größe der Beträge spielen eine Rolle. Deswegen gilt für die Additon ganzer Zahlen das Kommutativgesetz.
Die Gültigkeit des Kommutativgesetzes wird mit den folgenden beiden Tabelle für alle sechs Fälle an Beispielen verdeutlicht. Die rechte Tabelle notiert alle Terme in Kurzschreibweise.
|
|
Die rechte Tabelle zeigt, worauf beim Vertauschen von Summanden zu achten ist:
- Das negative Vorzeichen, das teilweise in dem Rechenzeichen „–“
versteckt ist, muss unbedingt zusammen
mit dem Betrag des Summanden den Platz wechseln, wenn der Wert
des Terms im Sinne des Kommutativgesetzes erhalten bleiben soll.
- Warnung: 11 – 6 ≠ 6 – 11 ; –10 + 7 ≠ –7 + 10
- 6 – 11 hat das entgegengesetzte Vorzeichen von 11 – 6
; das gleiche gilt für –10 + 7 und –7 + 10 .
- Es ist immer ein schwerer Fehler, wenn bei einer Umformung eines
Terms ein Vorzeichen von dem zugehörigen Betrag abgetrennt und dadurch
eine Zahl „zerrissen“ wird.
  |
Assoziativgesetz | |||
Der Abschnitt ist noch nicht besetzt.