mathebellus 5
	Subtraktion natürlicher Zahlen / Negative Zahlen
	Begriffe
	Pfeildiagramme
	Negative Ergebnisse
	Positive und negative Zahlen
	Betrag einer Zahl
	Gegenzahl einer Zahl
	Darstellung der Subtraktion als Addition

	Begriffe

Das Wort „subtrahieren“ ist aus der lateinischen Sprache entlehnt: „trahere“ bedeutet „ziehen/schleppen“ (Ein „Traktor“ ist ein „Schlepper“); „subtrahere“ bedeutet „wegziehen/abziehen“.

Die Zahl, von der etwas subtrahiert wird, heißt „Minuend“; die Zahl die abgezogen werden soll, heißt „Subtrahend“; das Ergebnis der Subtraktion heißt „Differenz“.

34	–	18	=	16
Minuend	minus	Subtrahend	gleich	Differenz

• Das lateinische Wort „minuere“ bedeutet „verringern/vermindern; ein „Minuend“ ist eine Zahl, die vermindert werden soll.
   
  
• Ein „Subtrahend“ ist eine Zahl, die abgezogen werden soll.
   
  
• Wort „Differenz“ ist von dem lateinischen Wort „differre“ abgeleitet, welches „sich unterscheiden“ bedeutet. Eine „Differenz“ ist also ein „Unterschied“.

	Pfeildiagramme

Eine Subtraktion natürlicher Zahlen lässt sich wie eine Addition durch ein Pfeildiagramm veranschaulichen:

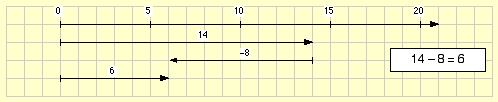
• Der Pfeil, der den Minuenden darstellt, beginnt bei 0; seine Länge ist durch den Wert des Minuenden gegeben (im Beispiel: 14).
   
  
• Der Pfeil, der den Subtrahenden darstellt, beginnt wie bei der Addition an der Spitze des ersten Pfeiles; seine Länge ist durch den Wert des Subtrahenden gegeben (im Beispiel: 8). Im Gegensatz zur Addition zeigt jedoch der Subtrahendenpfeil in die entgegengesetzte Richtung, dorthin, wo die Zahlen kleiner werden.
   
  
• Der Pfeil, der die Differenz darstellt, entsteht (wie bei der Addition) durch Aneinanderhängen der beiden Pfeile des Minuenden und des Subtrahenden; er beginnt daher bei 0 und endet an der Spitze des zweiten Pfeiles (im Beispiel: 6).
  

	Negative Ergebnisse

Ist der Subtrahend größer als der Minuend, ragt der nach links gerichtete Pfeil über die Zahl 0 hinaus. Um auch in diesem Fall ein Subtraktionsergebnis angeben zu können, verwenden wir wie bei einem Thermometer ein Spiegelbild des Zahlenstrahls:

Mit dieser Erweiterung des Zahlenstrahls werden neue Zahlen geschaffen, die sich durch ein Vorzeichen von den bisher bekannten Zahlen unterscheiden.

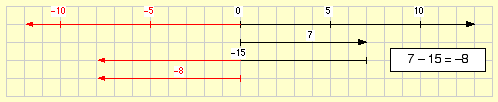
Das Wort „Strahl“ ist ein mathematischer Fachbegriff; es bezeichnet eine gerade Linie, die von einem Anfangspunkt ausgeht und kein Ende hat.
Mit der vorgenommenen Erweiterung ist der Zahlenstrahl kein Strahl mehr, weil er keinen Anfangspunkt besitzt; er ist zu einer Linie geworden, die in beiden Richtungen endlos ist.
Eine gerade Linie, die keine Endpunkte besitzt, sondern in beiden Richtungen endlos ist, wird in der Mathematik „Gerade“ genannt.
Aus dem Zahlenstrahl ist daher durch die Erweiterung die Zahlengerade geworden.

	Positive und negative Zahlen

Die neuen Zahlen, die durch Spiegelung des Zahlenstrahls am Nullpunkt entstehen, heißen negative Zahlen. Zur Kennzeichnung erhalten sie ein Minuszeichen. Das Wort „negativ“ stammt von dem lateinischen Verb „negare“ („verneinen“) ab.

Die alten Zahlen heißen positive Zahlen. Zur besseren Unterscheidung erhalten sie ein Pluszeichen. Dieses Pluszeichen wird jedoch häufig aus Bequemlichkeit weggelassen.

Die Zahl 0 ist einzige Zahl, die weder positiv noch negativ, sondern neutral ist. Die Zahl 0 besitzt kein Vorzeichen.


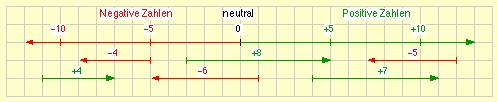
Die Abbildung zeigt, dass Zahlen nicht nur als „Stellen“ auf der Zahlengerade, sondern auch als „Pfeile“ wiedergegeben werden können.

• Pfeile, die nach rechts zeigen, veranschaulichen positive Zahlen.
• Pfeile, die nach links zeigen, veranschaulichen negative Zahlen.

	Betrag einer Zahl

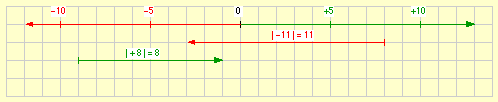
Wird von einer positiven oder einer negativen Zahl das Vorzeichen weggelassen, erhält man eine „alte“ Zahl, die „Betrag“ der positiven oder negativen Zahl genannt wird:

• Der Betrag von –17 ist 17.
• Der Betrag von +23 ist 23.
  

Es ist üblich, mit zwei senkrechten Strichen, die die Zahl einschließen, anzuzeigen, dass ihr Betrag gebildet werden soll:

• | –17 | = 17
• | +23 | = 23
  

Die beiden vorangehenden Zeilen werden genauso gelesen wie die beiden weiter oben stehenden.

Weil eine Zahl ohne Vorzeichen auch als Zahl mit dem Vorzeichen + angesehn werden kann, zeigen die beiden Beispiele zeigen:

• Der Betrag einer negativen Zahl wird gebildet, indem das negative Vorzeichen durch das positive ersetzt wird.
• Der Betrag einer positiven Zahl stimmt mit der Zahl selber überein.

Werden Zahlen als Stellen auf der Zahlengeraden veranschaulicht, so gibt der Betrag einer Zahl ihren Abstand von der Stelle 0 an:


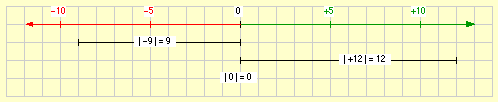
Werden Zahlen als Pfeile veranschaulicht, so gibt der Betrag einer Zahl die Länge des Pfeiles an:

	Gegenzahl einer Zahl

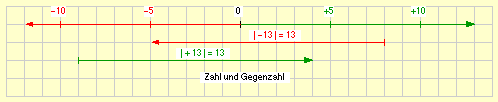
Zu jeder Zahl, die Zahl 0 ausgenommen, gibt es genau eine Zahl, die denselben Betrag, aber das entgegengesetzte Vorzeichen besitzt. Diese Zahl wird Gegenzahl der Zahl genannt.

• Die Gegenzahl von –17 ist +17.
• Die Gegenzahl von +23 ist –23.
  

Weil eine Zahl und ihre Gegenzahl denselben Betrag besitzen, sind die Stellen von Zahl und Gegenzahl auf der Zahlengeraden stets gleich weit von der Stelle 0 entfernt.


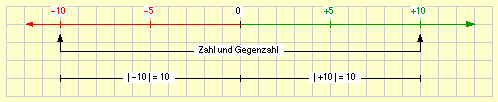
Weil eine Zahl und ihre Gegenzahl denselben Betrag besitzen, haben die Pfeile, die Zahl und Gegenzahl veranschaulichen, stets dieselbe Länge.

	Darstellung der Subtraktion als Addition

Mit den getroffenen Vereinbarungen können wir die Rechenart „Subtraktion“ vollständig durch die Rechenart „Addition“ ersetzen. Das zeigen die Pfeildiagramme weiter oben:
In beiden Pfeildiagrammen wird die Subtraktion ausgeführt, indem an den Minuenden wie bei einer Addition ein Pfeil angehängt wird. Allerdings gehört der Pfeil zur Gegenzahl des Subtrahenden, weil er in die entgegengesetzte Richtung zeigt.

Allgemein können wir deswegen sagen:

• Ein Subtrahend wird von einem  Minuenden subtrahiert, indem die Gegenzahl des Subtrahenden zu dem Minuenden addiert wird.
• Kurz: Subtrahieren ist Addieren der Gegenzahl.