|
mathebellus
5 |
|
| Addition natürlicher Zahlen |
 |
|
| Begriffe |
||
 |
Pfeildiagramme |
|
 |
Regeln, auf denen das Kopfrechnen
beruht |
|
 |
Das
Kommutativgesetz |
|
 |
Das
Assoziativgesetz |
|
 |
  |
Begriffe |
|||
Das Wort „addieren“ ist aus der lateinischen Sprache entlehnt: „addare“ bedeutet „hinzufügen“.
Die Zahlen, die zu addieren sind, heißen „Summanden“; das Ergebnis der Addition heißt „Summe“.
| 34 |
+ |
18 |
= |
52 |
| Summand |
plus |
Summand |
gleich |
Summe |
Das Wort „Summe“ ist von dem lateinischen Wort „summa“ abgeleitet, welches „Gesamtheit“ bedeutet.
Das Wort „Summand“ ist ein deutsches Kunstwort, das in Anlehnung an lateinischen Sprachregeln gebildet wurde; ein „numerus summandus“ ist eine Zahl, die „summiert werden soll“.
  |
Pfeildiagramme |
|||
Eine Addition natürlicher Zahlen lässt sich durch ein Pfeildiagramm veranschaulichen:
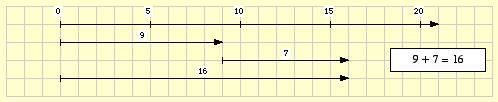
- Der Pfeil, der den ersten Summand darstellt, beginnt bei 0; seine
Länge ist durch den Wert des ersten Summanden gegeben (im Beispiel: 9).
- Der Pfeil, der den zweiten Summanden darstellt, beginnt an der
Spitze des ersten Pfeiles; seine Länge ist durch den Wert des zweiten
Summanden gegeben (im Beispiel: 7).
- Der Pfeil, der die Summe darstellt, entsteht durch Aneinanderhängen der beiden
Summandenpfeile; er beginnt daher bei 0 und endet an der Spitze des
zweiten Pfeiles (im Beispiel: 16).
  |
Regeln, auf denen das
Kopfrechnen beruht |
|||
Beim Addieren mehrstellige Zahlen im Kopf werden die Zahlen in Stellenwerte zerlegt, neu geordnet, die Stellenwerte getrennt addiert und abschließend wieder zu einer Zahl zusammengefügt:
| 340 + 590 | ||
| = (300 + 40) + (500 + 90) | Zahlen in Stellenwerte zerlegen |
|
| A+ |
= 300 + 40 + 500 + 90 | Klammern weglassen |
| K+ | = 300 + 500 + 40 + 90 | Summanden vertauschen |
| A+ | = (300 + 500) + (40 + 90) | Klammern setzen |
| = 800 + 130 | Addieren der Stellwerte |
|
| = 930 | Teilsummen zusammenfügen |
|
Das Kommutativgesetz (K+) gestattet uns, die Anordnung der Summanden abzuändern.
  |
Kommutativgesetz (K+) |
|||
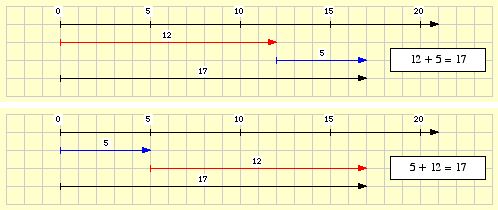
Die Reihenfolge, in der Summanden notiert werden, beeinflusst den Wert einer Summe nicht:
Sind a und b zwei natürliche Zahlen, so
gilt a + b = b + a .
Wir sagen: „Bei der Addition natürlicher Zahlen gilt das Kommutativgesetz.“ Das Kommutativgesetz erlaubt das Vertauschen von Summanden.
Beispiel:
12 + 5 = 17
5 + 12 = 17
5 + 12 = 17
  |
Assoziativgesetz (A+) |
|||
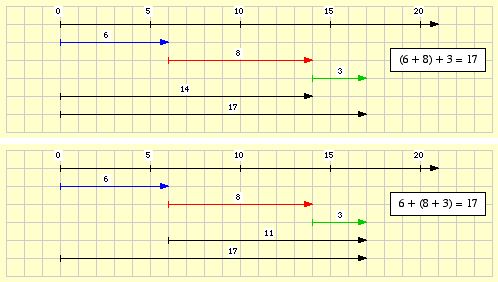
Die Reihenfolge, in der Summanden addiert werden, beeinflusst den Wert einer Summe nicht:
Sind a, b und c drei natürliche Zahlen,
so
gilt (a + b) + c = a + (b + c) .
Wir sagen: „Bei der Addition natürlicher Zahlen gilt das Assoziativgesetz.“ Das Assoziativgesetz erlaubt das Verbinden von Summanden zu Teilsummen. Daher darf beim Addieren die Rechenreihenfolge frei gewählt werden.
Beispiel:
6 + (8 + 3) = 6 + 11 = 17
(6 + 8) + 3 = 14 + 3 = 20
(6 + 8) + 3 = 14 + 3 = 20