mathebellus 5
	Die ganzen Zahlen und ihre Anordnung
	Die ganzen Zahlen
	Definition der Größer-Beziehung zwischen natürlichen Zahlen
	Übertragung der Definition der Größer-Beziehung auf ganze Zahlen

	Die ganzen Zahlen

Die (positiven) natürlichen Zahlen bilden zusammen mit all ihren negativen Gegenzahlen und der Zahl 0 die Menge der ganzen Zahlen.

Ganze Zahlen sind beispielsweise:  +4933 ; 0 ; –23576

Keine ganzen Zahlen sind: 1,5 ; π ; ³/₄ ; –12,3

Die ganzen Zahlen werden durch Stellen auf einer Geraden veranschaulicht. Diese Stellen werden gewonnen, indem, ausgehend von einem festgelegten Nullpunkt, in jeweils gleichem Abstand schrittweise in beide Richtungen Markierungen abgetragen werden.

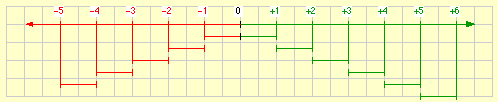
	Definition der Größer-Beziehung zwischen natürlichen Zahlen

Sind zwei natürliche Zahlen a und b gegeben, so kann ihre Differenz b – a gebildet werden; wir sagen: „Die Zahl b ist größer als die Zahl a“, wenn die Differenz  b – a  eine positive Zahl ist.
Anstelle von „b ist größer als a“ sagen wir auch: „a ist kleiner als b“.

Ist die natürliche Zahl b größer als die natürliche Zahl a, so schreiben wir:

• b > a    [gelesen: „b ist größer als a“]   oder
• a < b    [gelesen: „a ist kleiner als b”]
  

Beispiel:

• Es gilt  12 < 17 , weil  17 – 12 = 5  und 5 eine positive Zahl ist.
• Es gilt nicht  19 < 13, weil  13 – 19 = –6  und –6 eine negative Zahl ist.
• Es gilt nicht  15 < 15, weil  15 – 15 = 0  und 0 keine positive Zahl ist.
  

Veranschaulichung auf dem Zahlenstrahl:


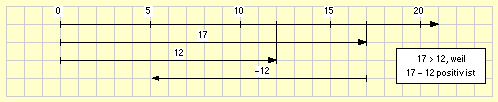
Das Schaubild zeigt, dass eine Zahl b genau dann größer als eine Zahl a ist, wenn sie auf dem Zahlenstrahl weiter rechts als die Zahl a liegt.

In diesem Fall ist der Pfeil, der den Subtrahenden a darstellt, kürzer als der Pfeil, der den Minuenden b darstellt. Wird dann an den Pfeil von b der Pfeil der Gegenzahl von a angehängt, ragt dieser nicht über die Stelle 0 in den negativen Bereich hinein.

	Übertragung der Definition der Größer-Beziehung auf ganze Zahlen

Sind nun zwei ganze Zahlen a und b gegeben, so sagen wir: „b ist größer als a“ oder: „a ist kleiner als b“, wenn b weiter rechts auf der Zahlengeraden als a liegt.


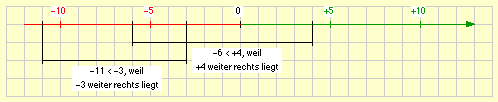
Aus den beiden im Schaubild dargestellten Beispielen wird deutlich, dass die Beträge zweier Zahlen in einer anderen Größenbeziehung stehen können als die Zahlen selber:

• –6 < +4 , obwohl  | –6 | > | +4 |
• –11 < –3 , obwohl  | –11 | > | –3 |
  

Die beiden Modelle, die wir für die ganzen Zahlen behandelt haben, stellen „Eselsbrücken“ für die Definition der Anordnung ganzer Zahlen bereit:

• –6 < +4 , weil eine Person mit 6 € Soll auf dem Konto ärmer als eine Person mit 4 € Haben auf dem Konto ist.
• –11 < –3 , weil eine Temperatur von –11°C kälter als eine Temperatur von –3°C ist.
  

Die Beziehung „größer“ kann in dem Modell der Kontostände durch die Beziehung „reicher” und in dem Modell der Temperaturen durch die Beziehung „wärmer“ veranschaulicht werden.

Wegen getroffenen Vereinbarung über die Anordnung der ganzen Zahlen, erhält die Zahlengerade zukünftig nur noch eine Pfeilspitze (s.o.). Die Bedeutung dieser Pfeilspitze ist also nicht etwa „Immer so endlos weiter!“ sondern: „In dieser Richtung werden die Zahlen größer!“