mathebellus 5
	Stellenwertsysteme
	Das Stellenwertprinzip
	Veranschaulichung durch Abpacken von Gegenständen
	Ziffern für Stellenwertsysteme - Kennzeichnung eines Stellenwertsystems
	Werte von Zahlen berechnen, die in einem anderen Stellenwertsystem notiert sind
	Zahlen in einem anderen Stellenwertsystem notieren (Umkehrung der Wertberechnung)
	Zahlen in einem anderen Stellenwertsystem notieren (Verfahren nach Euklid)
	mathecitor 012

	Das Stellenwertprinzip

In der römischen Schreibweise für Zahlen haben die benutzten Ziffern, unabhängig von der Stelle, an der sie stehen, immer dieselbe Bedeutung; beispielsweise hat die Ziffer „X“ in dem Zahlwort  CCXXIX  an allen drei Stellen immer die Bedeutung „zehn“. Deswegen ist die römische Zahlschreibweise kein Stellenwertsystem.

Im Gegensatz dazu hat aber die Ziffer „2“ in dem Zahlwort  229  zwei verschiedene Bedeutungen; an der von rechts gesehen zweiten Stelle bedeutet sie „zwanzig“, an der dritten „zweihundert“.

Der Grund dafür ist die folgende Vereinbarung (Stellenwertsystem):

• Der Wert der von rechts gesehen ersten Stelle ist „eins“; steht eine Ziffer an dieser Stelle, so wird ihr Wert einfach gezählt.
• Der Wert einer jeden anderen Stelle ist stets ein festgelegtes Vielfaches (normalerweise: das Zehnfache) des Wertes der vorangehenden Stelle.

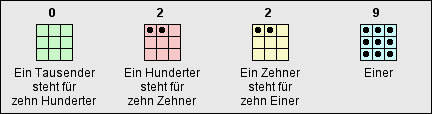
Die Anzahl der Ziffern, die man benötigt, um jede der unendlich vielen Zahlen aufschreiben zu können, ist so groß wie das festgelegte Vielfache, mit dem der Wert einer Stelle beim Übergang zur nächsten multipliziert wird.

Für das uns geläufige Stellenwertsystem, bei dem jede folgende Stelle den zehnfachen Wert der vorangehenden hat, benötigt man zehn Ziffern:

0   1   2   3   4   5   6   7   8   9

Für die Zahl „zehn“ benötigt man keine eigene Ziffer, weil ja diese Zahl durch eine 1 an der von rechts gesehen zweiten Stelle beschrieben werden kann:

10

Hier wird deutlich, dass es eine Ziffer 0 geben muss, die selber keinen Wert besitzt, mit der aber eine andere Ziffer an eine gewünschte Stelle gerückt werden kann.

Die Anzahl der Ziffern, die für ein bestimmtes Stellenwertsystem benötigt werden, heißt Basis des Stellenwertsystems. Unsere normale Zahlenschreibweise ist daher ein Stellenwertsystem mit der Basis „zehn“.

	Veranschaulichung eines Stellenwertsystems durch „Abpacken“ von Gegenstände

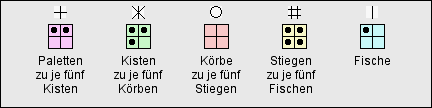
Es war einmal vor langer Zeit ein Volk von Fischern, wir wollen sie „Pentonen“ nennen, die ihre Fänge stets wie folgt abpackten:

	Fünf Fische legten sie in eine Stiege.
	Fünf Stiegen stapelten sie in einen Korb.
	Fünf Körbe verstauten sie in einer Kiste.
	Fünf Kisten stellten sie auf eine Palette.
	Fünf Paletten setzten sie in ein Boot.

Um die Größe irgendeines Fischfangs zu beschreiben, benötigten die Pentonen folglich einen Vorrat von fünf Ziffern:

 („null“)     („eins“)     („zwei“)     („drei“)     („vier“)

Die „pentonische“ Zahl          bedeutet dann von rechts nach links gelesen:


Ein Fisch, vier Stiegen, null Körbe, drei Kisten und zwei Paletten ergeben zusammen 1646 Fische, weil

• eine Stiege fünf Fische,
• ein Korb fünf mal fünf, das heißt, fünfundzwanzig Fische,
• eine Kiste fünf mal fünf mal fünf, das heißt einhundertfünfundzwanzig Fische,
• eine Palette fünf mal fünf mal fünf mal fünf, das heißt sechshundertfünfundzwanzig Fische
• usw.
  

enthält. Die Pentonen benutzten offensichtlich ein Stellenwertsystem mit der Basis „fünf“, um ihre Fische zu zählen!

	Ziffern für Stellenwertsysteme - Kennzeichnung eines Stellenwertsystems

Ist die Basis kleiner als 10,

so werden üblicherweise die arabischen Ziffern, deren Wert kleiner als die Basis ist, verwandt, um eine Zahl in dem Stellenwertsystem zu notieren.

Ist die Basis größer als 10,

so werden zusätzlich, bei A beginnend, die erforderliche Anzahl von Buchstaben zu dem Vorrat an arabischen Ziffern hinzugefügt.

Weil in den verschiedenen Stellenwertsystemen immer dieselben arabischen Ziffern und nicht andere (z.B. pentonische) verwandt werden, um Zahlen  zu notieren, muss deutlich gemacht werden, welches Stellenwertsystem gerade betrachtet wird, denn sonst könnte ja zum Beispiel

10

die Zahl „zehn“ oder die Zahl „fünf“ oder die Zahl „sechzehn“ bezeichnen, je nachdem, welches Stellenwertsystem gerade zugrunde gelegt wird. Zur Vermeidung von Missverständnissen wird eine Zahlnotiz, die sich nicht auf das Zehnersystem bezieht, mit der Basis wie folgt gekennzeichnet:

(10)₅     ein „Fünfer“
(10)₈     ein „Achter“

	Werte von Zahlen berechnen, die in einem anderen Stellenwertsystem notiert sind

Um den Wert einer Zahl zu berechnen, die in einem anderen Stellenwertsystem notiert ist, werden die Ziffern mit den Werten der Stellen multipliziert, auf denen sie stehen. Anschließend werden diese Produkte addiert.

(5236)₇

= 6*1 + 3*7 + 2*(7*7) + 5*(7*7*7)
= 6 + 21 + 98 + 1715
= 1840

(A15)₁₂

= 5*1 + 1*12 + 10*(12*12)
= 5 + 12 + 1440
= 1457

	Zahlen in einem anderen Stellenwertsystem notieren (Umkehrung der Wertberechnung)

Das erste Verfahren, eine Zahl in einem anderen Stellenwertsystem zu notieren, kehrt einfach die Wertberechnung um, die im vorangegangenen Abschnitt vorgestellt wurde.

• Es werden zunächst alle Stellenwerte betrachtet, die kleiner als die darzustellende Zahl sind.
• Dann wird (durch Division) überprüft, wie oft der größte dieser Stellenwerte in die Zahl hineinpasst. Das Ergebnis dieser Divison liefert die von links gesehen erste Ziffer.
• Anschließend wird geprüft, wie oft der Divisionsrest den zweitgrößten Stellenwert enthält. Das Ergbnis dieser zweiten Division liefert die von links gesehen zweite Ziffer (Diese kann auch 0 sein!).
• Das Divisionsverfahren wird solange wiederholt, bis der niedrigste Stellenwert 1 erreicht ist. Weil die Division durch 1 immer aufgeht, liefert der Rest der vorletzten Division zugleich die letzte Ziffer, die an der Einerstelle steht

Beispiele

Die Zahl 104 soll im Stellenwertsystem mit der Basis 3 („Dreiersystem“) dargestellt werden. Dazu müssen die Stellenwerte    1,   3,   9,   27   und   81  betrachtet werden. Der nächste Stellenwert  3*81 = 243  ist bereits zu groß.

104 = 1*81 + 23
23 = 0*27 + 23
23 = 2*9 + 5
5 = 1*3 + 2
2 = 2*1

104 = (10212)₃

Die Zahl 231 soll im Stellenwertsystem mit der Basis 16 („Sechzehnersystem“) dargestellt werden. Dazu müssen nur die Stellenwerte    1   und   16  betrachtet werden; denn der nächste Stellenwert  16*16 = 256  ist bereits zu groß.

231 = 14*16 + 7
7 = 7*1

231 = (E7)₁₆

	Zahlen in einem anderen Stellenwertsystem notieren (Euklidisches Verfahren)

Das zweite Verfahren, eine Zahl in einem anderen Stellenwertsystem zu notieren, geht auf den griechischen Mathematiker Euklid (365 bis 300 v.Chr.) zurück.

• Es wird die darzustellende Zahl durch die Basis dividiert; der Rest der Division gibt die von rechts gesehen erste Ziffer an, weil er der Bestandteil der Zahl ist, der bei der Aufteilung auf die Stellenwerte übrig bleibt.
• Das Ergebnis der Division wird erneut durch die Basis dividiert; der Rest der zweiten Division gibt die von rechts gesehen zweite Ziffer an, weil er der Bestandteil ist, der bei der Aufteilung auf die höheren Stellenwerte übrig bleibt.
• Das Divisionsverfahren wird solange wiederholt, bis das Ergebnis der Division 0 ist.

Beispiele

Die Zahl 1575 soll im Stellenwertsystem mit der Basis 8 („Achtersystem“) dargestellt werden. 

1575 = 196*8 + 7
196 = 24*8 + 4
24 = 3*8 + 0
3 = 0*8 + 3

1575 = (3047)₈

Die Zahl 231 soll im Stellenwertsystem mit der Basis 16 („Sechzehnersystem“) dargestellt werden.

231 = 14*16 + 7
14 = 0*16 + 14

231 = (E7)₁₆